Research

Dr. Vannucci is generally interested in the development of Bayesian statistical models for complex problems and applications to Science. Her methodological research has focused in particular on the development of wavelet-based models for functional data, on the theory and practice of Bayesian variable selection techniques, and on graphical models. Dr. Vannucci’s methodological research is often motivated by real problems that need to be addressed with suitable statistical methods. She has a solid history of scientific collaborations and is keenly interested in large-scale genomics and neuroscience, particularly neurology and neuroimaging.

Theory & Methods: Bayesian inference, Graphical models, Nonparametric Bayes, Statistical computing, Variable selection and Wavelets.

Applications: Engineering, Large-scale Genomics, Neurology, Neuroimaging & Neuroscience.

Dr. Vannucci’s main methodological contributions have included:

Dr. Vannucci has contributed innovative Bayesian models for wavelet shrinkage with random wavelet coefficients, incorporating efficient algorithms for the computation of their covariances; for wavelet-based regression modeling of functional data, including curve regression and hierarchical models; and for classification models based on functional data. Other work has broadly related to the modeling of time series data, with various applications.

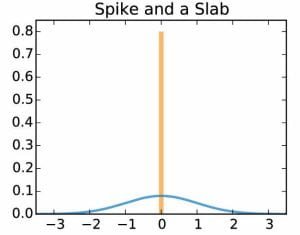
Dr. Vannucci has contributed original approaches to Bayesian variable selection in multivariate regression models, extending models that use mixture prior distributions with a spike at zero, and investigating efficient stochastic search MCMC algorithms that cleverly deal with the changing dimension of the parameter space; innovative ways to perform Bayesian variable selection for sample clustering, with both finite and infinite mixture models; and extensions to various modeling settings for non-Gaussian (e.g., categorical, count and compositional) data. Other methodological contributions to Bayesian variable selection have included explorations of priors that incorporate point masses in nonparametric constructions.

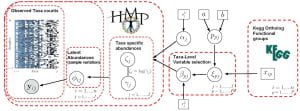A particular focus of Dr. Vannucci’s work has been in the development of integrative models that combine multiple data types, for dedicated applications to large-scale genomics (e.g., DNA microarray, proteomics), imaging genetics and  microbiome studies. The development of these complex models has often been coupled with innovative variable selection prior constructions, that account for specific dependence structures in the data (e.g., spatial and network relationships), and efficient sampling algorithms for posterior inference.

Dr. Vannucci has developed innovative Bayesian models for the estimation of multiple graphs in situations where some of the graphs may be unrelated, while others share common features. Attention has been given to prior constructions that allow to share information between graphs, when appropriate. Other contributions have been in the development of robust modeling and in latent graphical modeling settings for non-Gaussian data, with efficient implementations that employ variational schemes.

Dr. Vannucci’s main interdisciplinary efforts have included:

Dr. Vannucci’s methodological innovations in neuroimaging include innovative spatio-temporal Bayesian models for the detection of activated brain regions in task-based fMRI studies, and multi-subject vector autoregressive (VAR) models for the estimation of brain connectivity networks, e.g., how brain regions interact and share information with each other. Methods were implemented via scalable variational Bayes algorithms and standalone user-friendly MATLAB GUIs, to facilitate adoption from the broader community. Other contributions include integrative models for  multi-modal data and original principled Bayesian approaches for the estimation of dynamic, e.g, time-varying, brain connectivity.  Methodological developments have been motivated and supported by several interdisciplinary collaborations, e.g, in epilepsy and traumatic brain injury research, and by behavioral and cognitive studies.

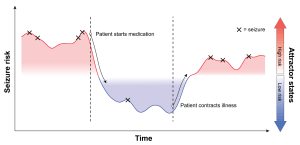
As co-leader, with former student Sharon Chiang (Ph.D./M.D.), of an interdisciplinary team in epilepsy research, Dr. Vannucci has shown how seizure risk of epileptic patients can be estimated as a latent quantity based on their seizure counts. Approaches she has developed include novel hidden Markov models with variable selection priors, for the identification of drivers of seizure risk cycles, and dynamical system frameworks to better understand and predict the timing of seizures. Methods have also been extended to the analysis of data from surgically implanted devices for brain neurostimulation.

 

Together with 9 other authors, Dr. Vannucci has contributed to the highly cited article “Bayesian Statistics and Modeling”, appeared in 2021 as article 1 in vol. 1 of Nature Reviews Methods Primer.

 

Dr. Vannucci is co-editor  (with Mahlet G. Tadesse) of the 2021 Handbook of Bayesian Variable Selection,  published by Chapman & Hall/CRC. The book is a comprehensive review of theoretical, methodological and computational aspects of Bayesian variable selection methods, spanning over 30 years of research on these topics.

 

Dr. Vannucci is co-editor  (with Sharon Chiang and Vikram Rao) of the 2024 Statistical Methods in Epilepsy edited volume,  published by Chapman & Hall/CRC. The book provides a comprehensive introduction to statistical methods employed in epilepsy research, as a practical roadmap for learners and experts alike.

 

 

See  here for a complete list of Dr. Vannucci’s papers.

Dr. Vannucci’s research has been supported by: